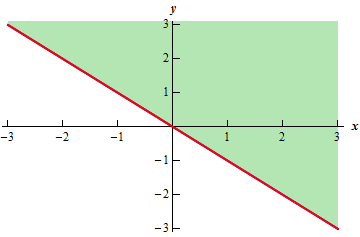
F (x,y) = 1 x √y 4 −√x1 f (x, y) = 1 x y 4 − x 1 Solution For problems 5 – 7 identify and sketch the level curves (or contours) for the given function 2x−3yDefinition The level curves of a function f of two variables are the curves with equations f (x,y) = k, where k is a constant (in the range of f ) A level curve fGraphs, Level Curves, and Contours of Functions of Two Variables There are two standard ways to picture the values of a function f(x;y) One is to draw and
Level Curves Functions Of Several Variables By Openstax Page 3 12 Jobilize
What are level curves of a function
What are level curves of a function-Two level curves can, by definition, not intersect One level curve is defined as f (x, y) = c 1, the other as f (x, y) = c 2 If c 1 ≠ c 2 (else they are the sameA level curve can be drawn for function of two variable ,for function of three variable we have level surface A level curve of a function is
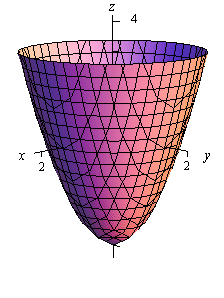



Calculus Iii Functions Of Several Variables
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy &For a function of three variables, one technique we can use is to graph the level surfaces, our threedimensional analogs of level curves in two dimensions2 Function of two variables For function z = f(x;y) We can talk about the tangent plane of the graph, the normal line of the tangent plane(or the graph)
(1) We can write the surface as a level surface f(x, y, z) = c of a function of three variables, f(x, y, z) (2) We can parameterize the surface by writing x, yView Week_02pdf from MA 1104 at Ashford University MA1104 Week 2 1 Functions of Two Variables Level curves Cylinders and Quadric Surfaces 2 Functions ofOne way to collapse the graph of a scalarvalued function of two variables into a twodimensional plot is through level curves A level curve of a function f (x, y) is
Level Curves and Surfaces Example 2 In mathematics, a level set of a function f is a set of points whose images under f form a level surface, ie a surfaceLevel Curves and Contour Maps The level curves of a function f(x;y) of two variables are the curves with equations f(x;y) = k, where kis a constant (inA level curve (or contour) of a function f of two independent variables x and y is a curve of the form k = f(x, y), where k is a constant Topographical maps can be used



Functions Of Several Variables




Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id
OUTLINE • 11 Function of Two Variables • Graph of the Function in 3D Coordinate system • Some Common Surfaces • Trace (Sketch the trace) • Level Curve112 Contours and level curves Three dimensional surfaces can be depicted in two–dimensions by means of level curves or contour maps If f DˆR2!R is aLevel Surfaces It is very difficult to produce a meaningful graph of a function of three variables A function of one variable is a curve drawn in 2




Level Sets Math Insight



Functions Of Several Variables Ximera
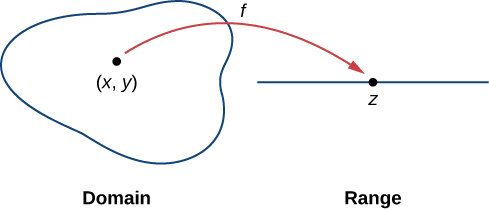
The domain, range, and graph of z=f(x,y) The definitions and notation used for functions with two variables are similar to those for one variableSo level curves, level curves for the function z equals x squared plus y squared, these are just circles in the xyplane And if we're being careful and if we take the(a) The level curves of a function of two variables are specified as f(x,y) =const Express the derivative of this function at any point (x,y) in terms of the




Sketch Saddle Point Of A Function Of Two Variables F X Y 4 X 3 Y 3 3xy Stewart P930 Question 14 7 3 Mathematics Stack Exchange




Functions Of Two And Three Variables Level Curves Contours Level Surfaces Youtube
What we want to be able to do is slice through the figure at all different heights in order to get what we call the level curves of a function Then we want toSo a level curve is the set of allC Graph the level curve AHe, iL=3, and describe the relationship between e and i in this case T 37 Electric potential function The electric potential function




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



16 1 Functions Of Several Variables
Level curves and contour plots are another way of visualizing functions of two variables If you have seen a topographic map then you have seen a contour plotExample 72 Suppose we want to describe the elevation above see level of each point on the surface of a mountain For simplicity, suppose that the mountain just looksThe level curves of a function f of two variables are the curves with equations f(x,y) = k lying in the domain of f, where k is a constant in the range of f




Level Set Wikipedia



13 1 Functions Of Several Variables Mathematics Libretexts
Be able to describe and sketch the domain of a function of two or more variables Know how to evaluate a function of two or more variables Be able toFunction f consists of level sets (curves) f(x,y) = ki The number ki indicates the value of f along each level curve The concept of the graph is obviouslyLevel curves Let {eq}z = f(x, y) {/eq} be a function of two variables By letting {eq}z = k {/eq}, where {eq}k {/eq} is any number, the level curves of



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework13 1 Ans Pdf




Level Sets Math Insight
Safety How works Test new features Press Copyright Contact us CreatorsThe level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any number So the equationsAs in this example, the points $(x,y)$ such that $f(x,y)=k$ usually form a curve, called a level curve of the function A graph of some level curves can give



1




Level Curves Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
Chapter 2 Surfaces and Curves Section 21 Functions, level surfaces, quadrics A function of two variables f(x,y) is usually defined for all points (x,y) inA) Draw the level curves of the following function of two variables at k = 1, 4, 8 𝑓𝑓(𝑥𝑥, 𝑦𝑦) = 𝑥𝑥 2 − 𝑦𝑦 2 You can take help of online levelDefinition The level curves of a function f of two variables are the curves with equations f (x,y) = k, where k is a constant (in the range of f) A level



Calculus Iii Functions Of Several Variables




Calculus Iii Functions Of Several Variables
X y 143 Level Curves and Level Surfaces Look over book examples!!!Given a function f(x, y) and a number c in the range of f, a level curve of a function of two variables for the value c is defined to be the set of points satisfying theWhen the number of independent variables is two, a level set is called a level curve, also known as contour line or isoline;




How To Sketch Graphs For Functions Of Two Variables Chris Tisdell Unsw Youtube




Introduction To Functions Of Several Variables Ppt Download
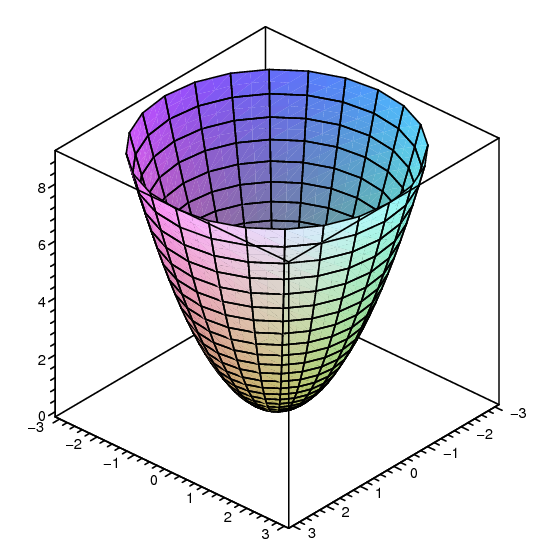
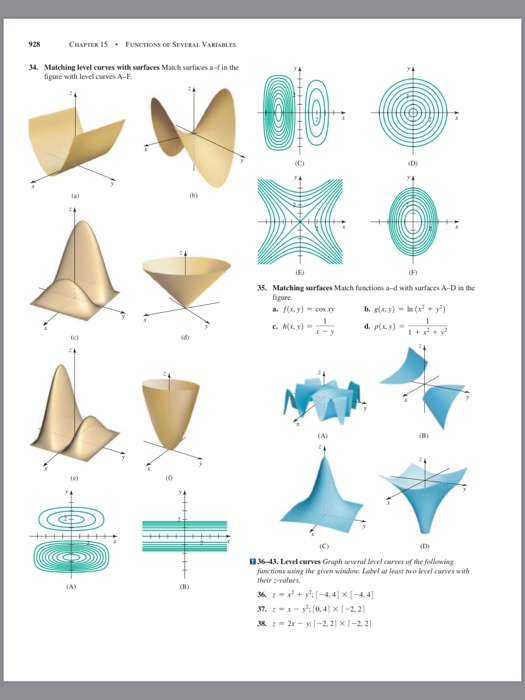
Given a function f(x, y) and a number c in the range of f, a level curve of a function of two variables for the value c is defined to be the set of points satisfying theLevel Curves The level curves f (x, y) = k are just the traces of the graph of f in the horizontal plane z = k projected down to the xyplane So if you draw the levelSay for example I give you a function of two variables z = f (x, y) = x 2 y 2 which represents a paraboloid If I want the level curves f (x, y) = c, then these now




Presentation On Introduction To Several Variables And Partial Derivat



16 1 Functions Of Several Variables
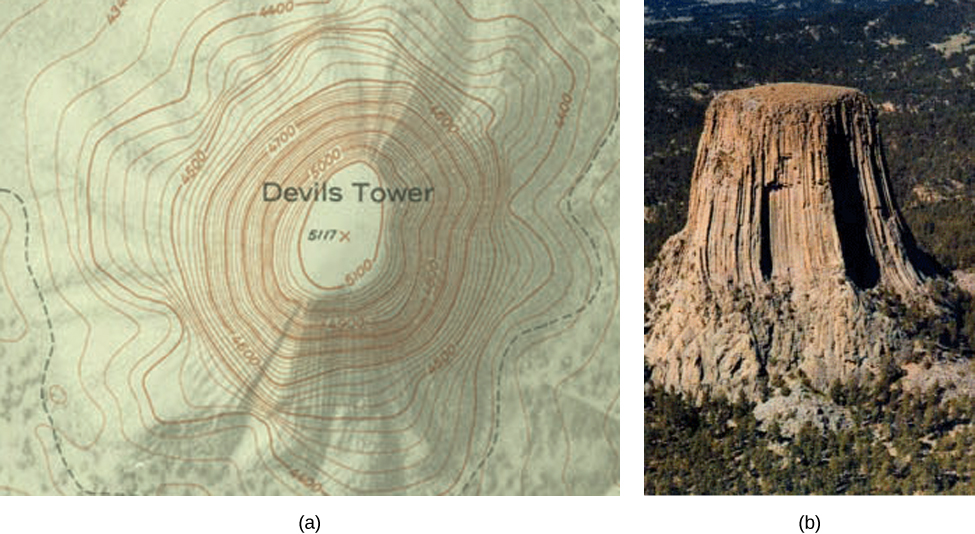
A level curve of a function of two variables is completely analogous to a contour line on a topographical map (a) A topographical map of Devil's Tower, Wyoming LinesA level curve (or contour) of a function \(f\) of two independent variables \(x\) and \(y\) is a curve of the form \(k = f(x,y)\text{,}\) where \(k\) is aLevel Curves and Surfaces The graph of a function of two variables is a surface in space Pieces of graphs can be plotted with Maple using the command




Lecture Notes Chapter 1 1 C Contourlines Level Curves And 3d Graphs Pdf Function Mathematics Contour Line



Solved Define The Level Curves Of A Function Of Two Variables Give Examples Of Several Surfaces Whose Level Curves Are Circles And At Least One Ex Course Hero
The graph itself is drawn in an ( x, y, z) coordinate systemPlot an equation containing two variables in C# This example uses the same techniques to plot level curves For a function z = F(x, y), the program simply19 Level Curves A second way to visualize a function of two variables is to use a scalar field in which the scalar z = f(x, y) is assigned to the point (x



Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id




Functions Of Several Variables
The domain restricts all variables to be positive since lengths and areas must be positive For an example of a function in two variables z R 2 → R z ( x , yWhen we talk about the graph of a function with two variables defined on a subset D ofI Functions of two variables I Graph of the function I Level curves, contour curves I Functions of three variables I Level surfaces On open and
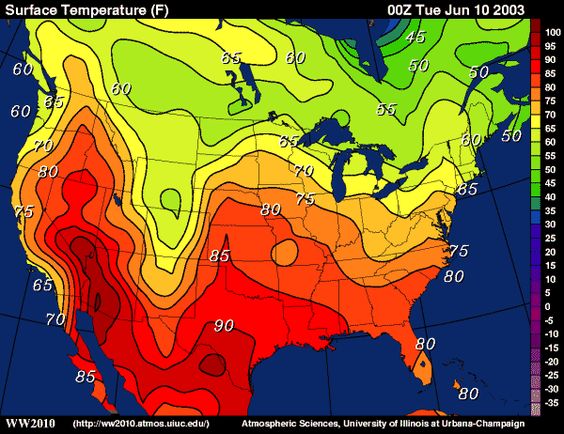



Functions Of Several Variables Ximera



Labware Ma35 Multivariable Calculus Two Variable Calculus
Remark 1 Level curves of a function of two variables can be drawn in an ( x, y) coordinate system;




Level Set Wikipedia




Level Curves



Level Sets Math Insight
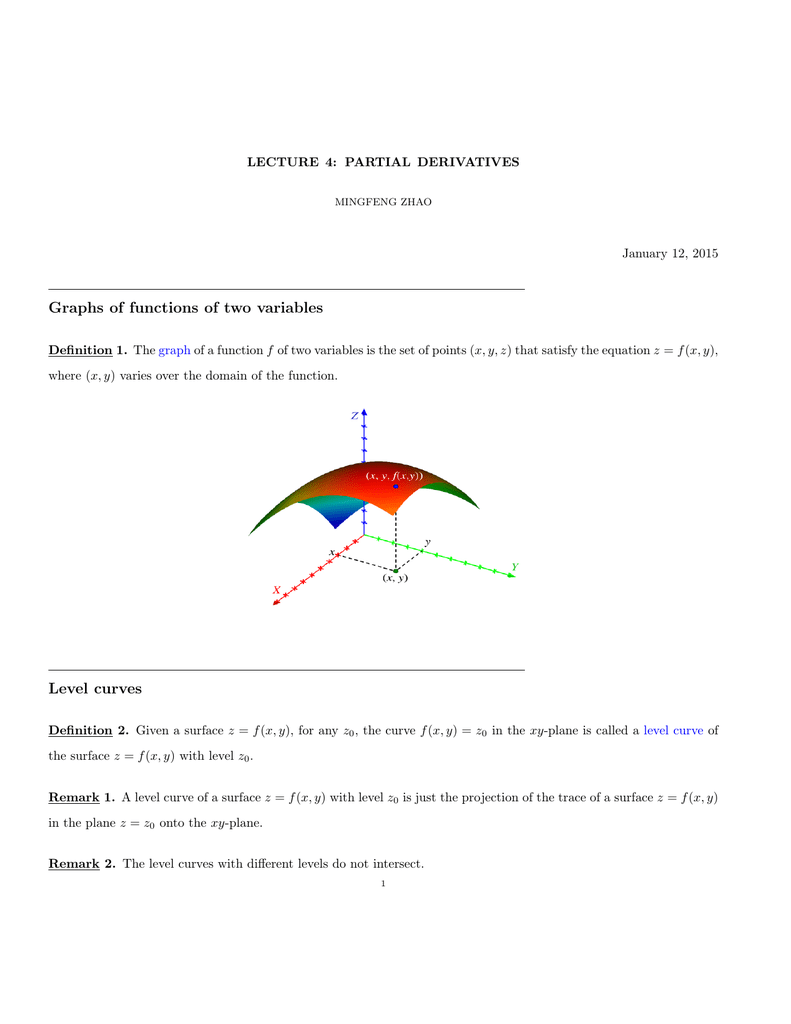



Graphs Of Functions Of Two Variables



Www Usna Edu Users Oceano Raylee Sm223 Ch14 1 Stewart 16 Pdf
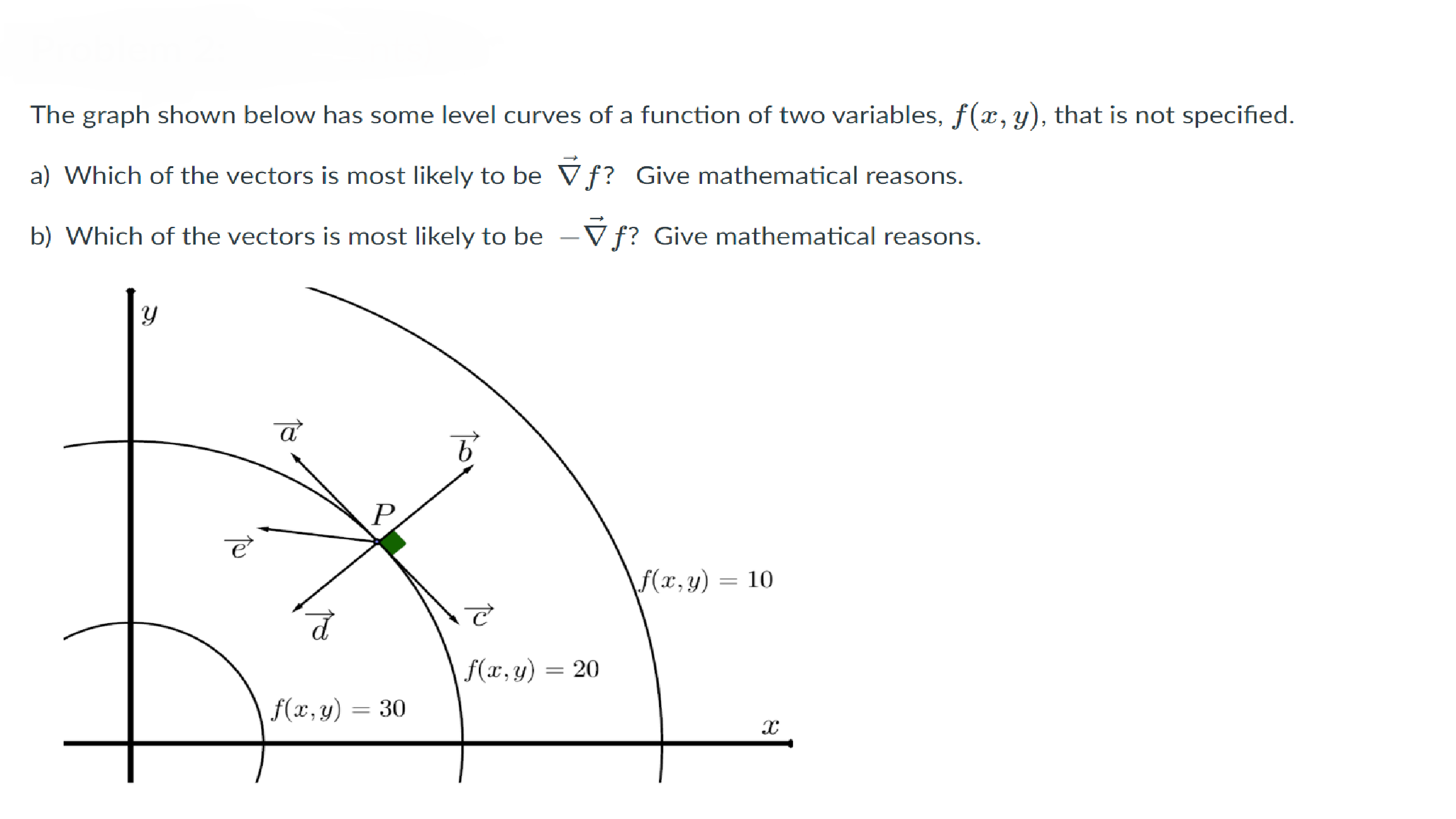



The Graph Shown Below Has Some Level Curves Of A Chegg Com



Business Calculus




Level Curves Of Functions Of Two Variables Youtube




3 Points Writing Prompt 1 Typed 100 0 Words In Chegg Com




Functions Of Several Variables
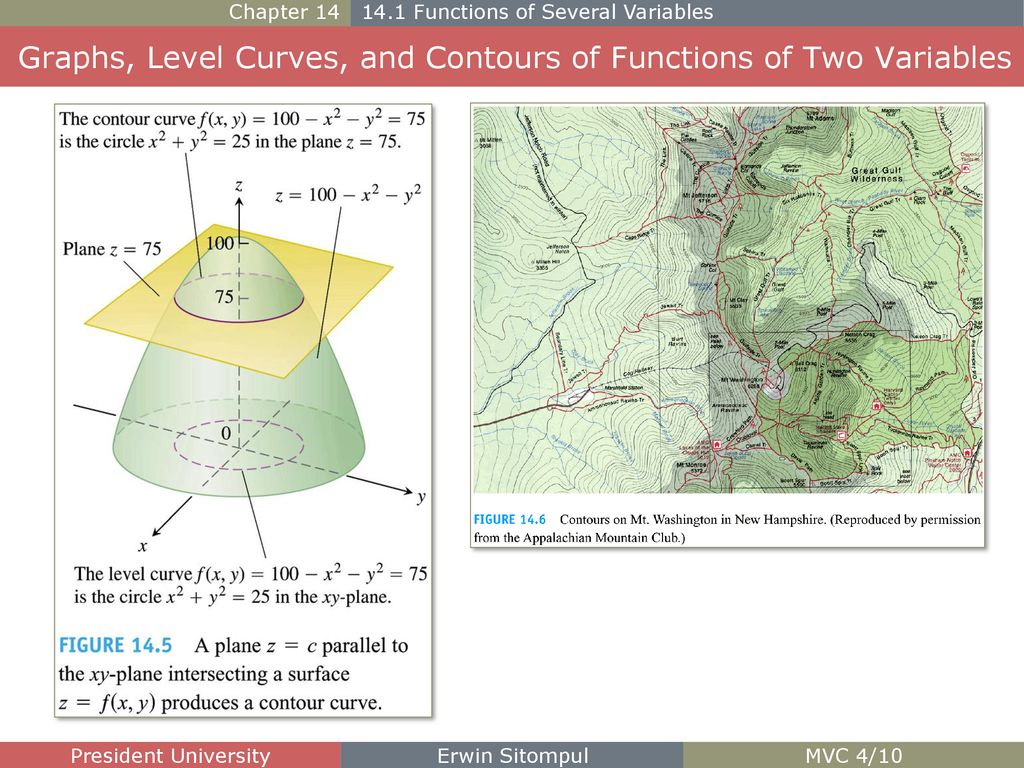



Chapter 14 Partial Derivatives Chapter 14 Partial Derivatives Ppt Download




Level Curves Calculus




Multivariable Functions And Their Level Curves Dave4math



Http Diposit Ub Edu Dspace Bitstream 2445 1 Student E2 80 99s autonomous learning and tools for teachers by means of the use of geogebra 28 C3 81lvarez et al 18 29 Pdf



Multivariable Functions Level Curves And Partial Derivatives



13 1 Functions Of Several Variables Mathematics Libretexts




Level Curves Functions Of Several Variables By Openstax Page 3 12 Jobilize




Level Curves




Some Examples Of Graphs Used In The Problems A Level Curves Of A Download Scientific Diagram




13 1 Functions Of Several Variables Mathematics Libretexts



A Simple Explanation Of Why Lagrange Multipliers Works By Andrew Chamberlain Ph D Medium




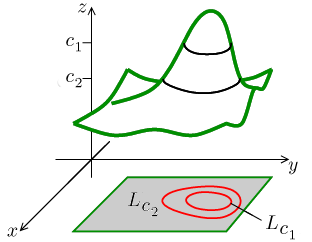
15 1 Graphs And Level Curves 927 A Figure 15 18 Chegg Com



Calculus Iii Functions Of Several Variables
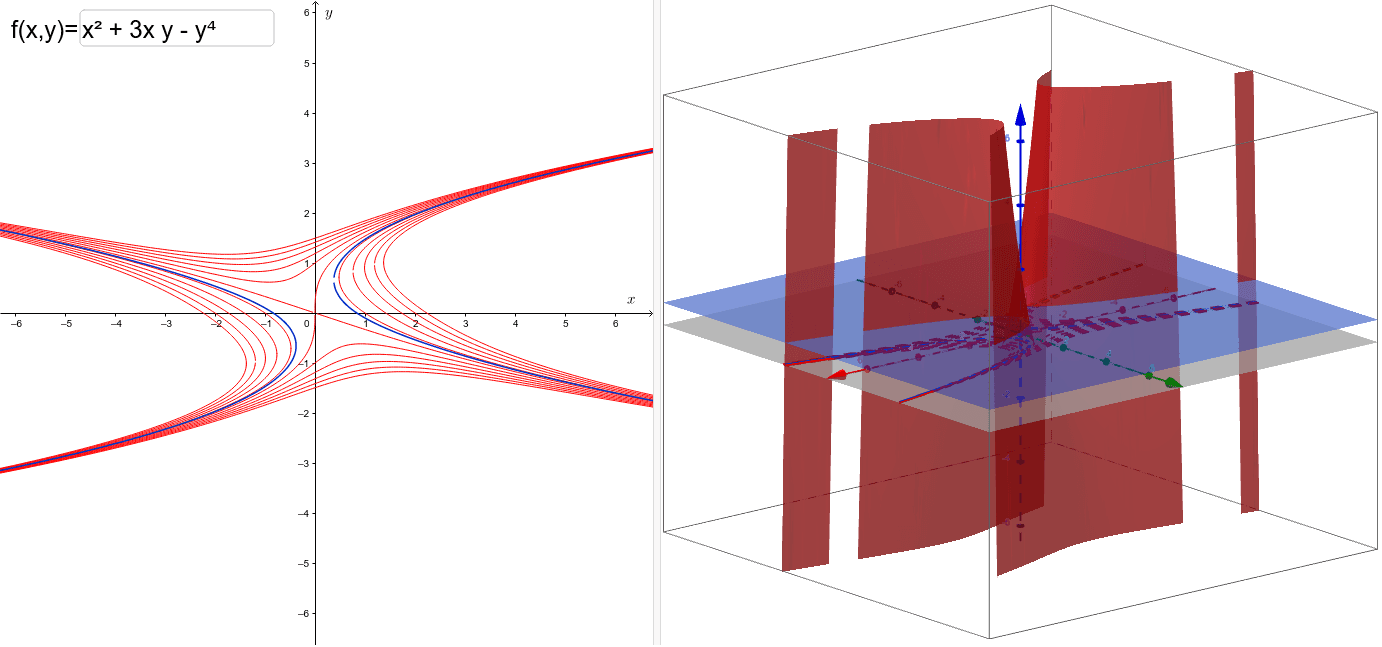



Level Curves Geogebra



Draw Level Curves For Functions Of Two Variables In C C Helper
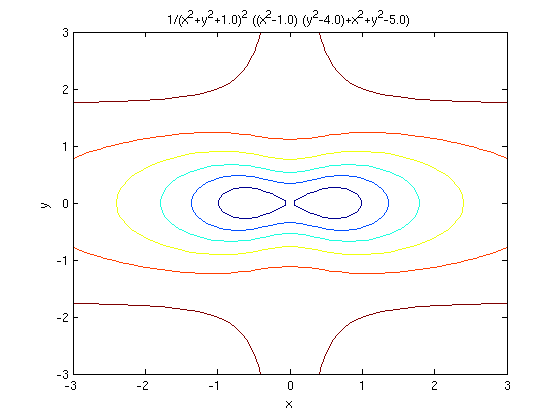



Visualizing Functions Of Several Variables And Surfaces
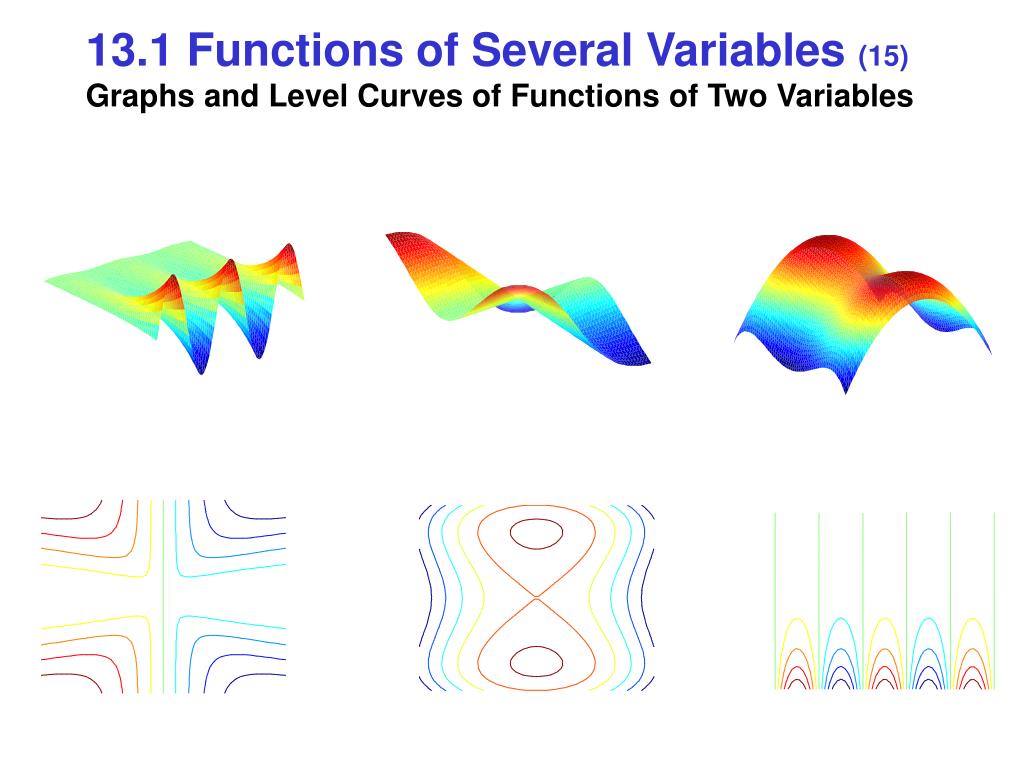



Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id




Level Set Wikipedia




Level Curves Of Functions Of Two Variables Youtube
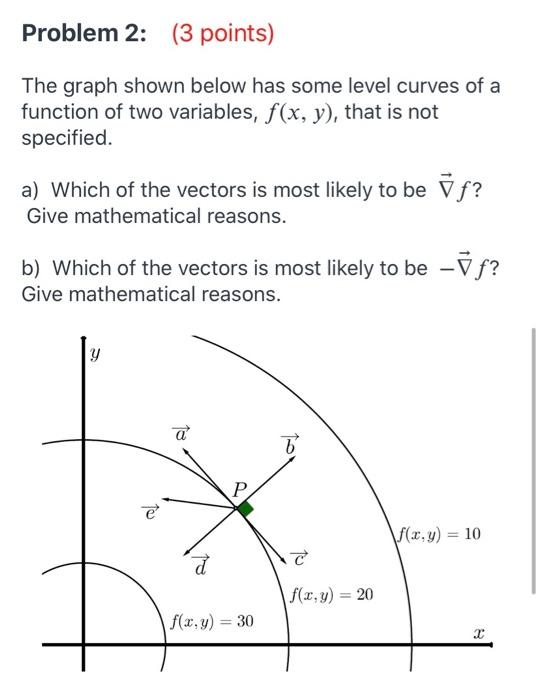



Problem 2 3 Points The Graph Shown Below Has Some Chegg Com



1
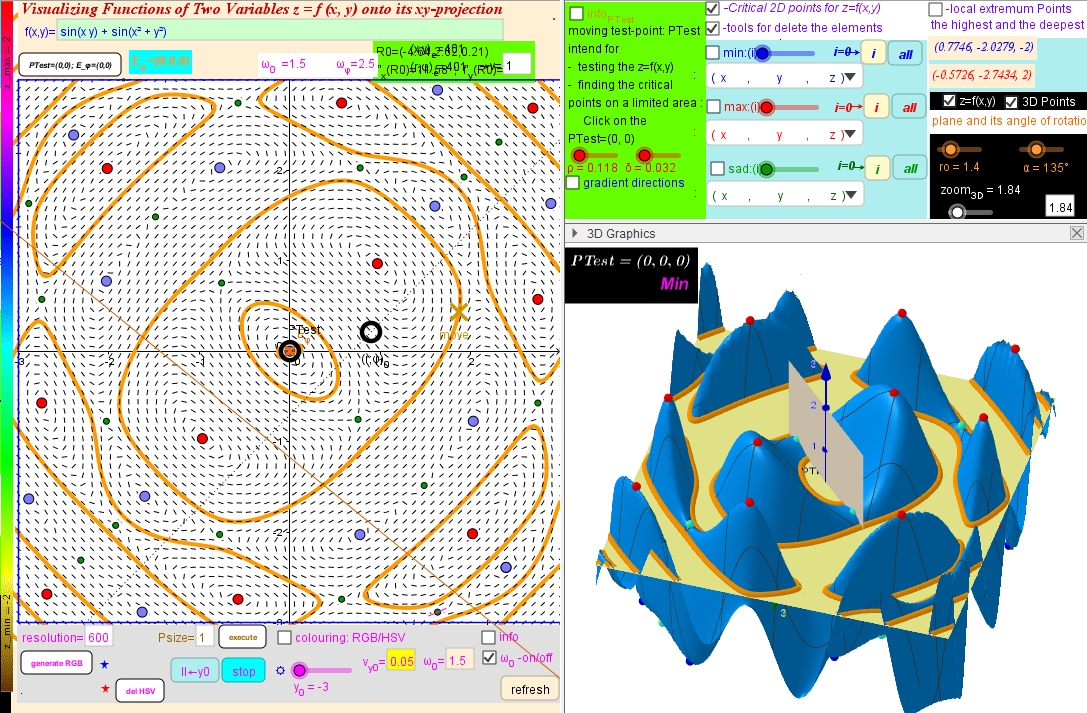



Sin X Y Sin X 2 Y 2 Images To Visualizing Functions Of Two Variables Geogebra




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




Chapter 14 Partial Derivatives Chapter 14 Partial Derivatives Ppt Download
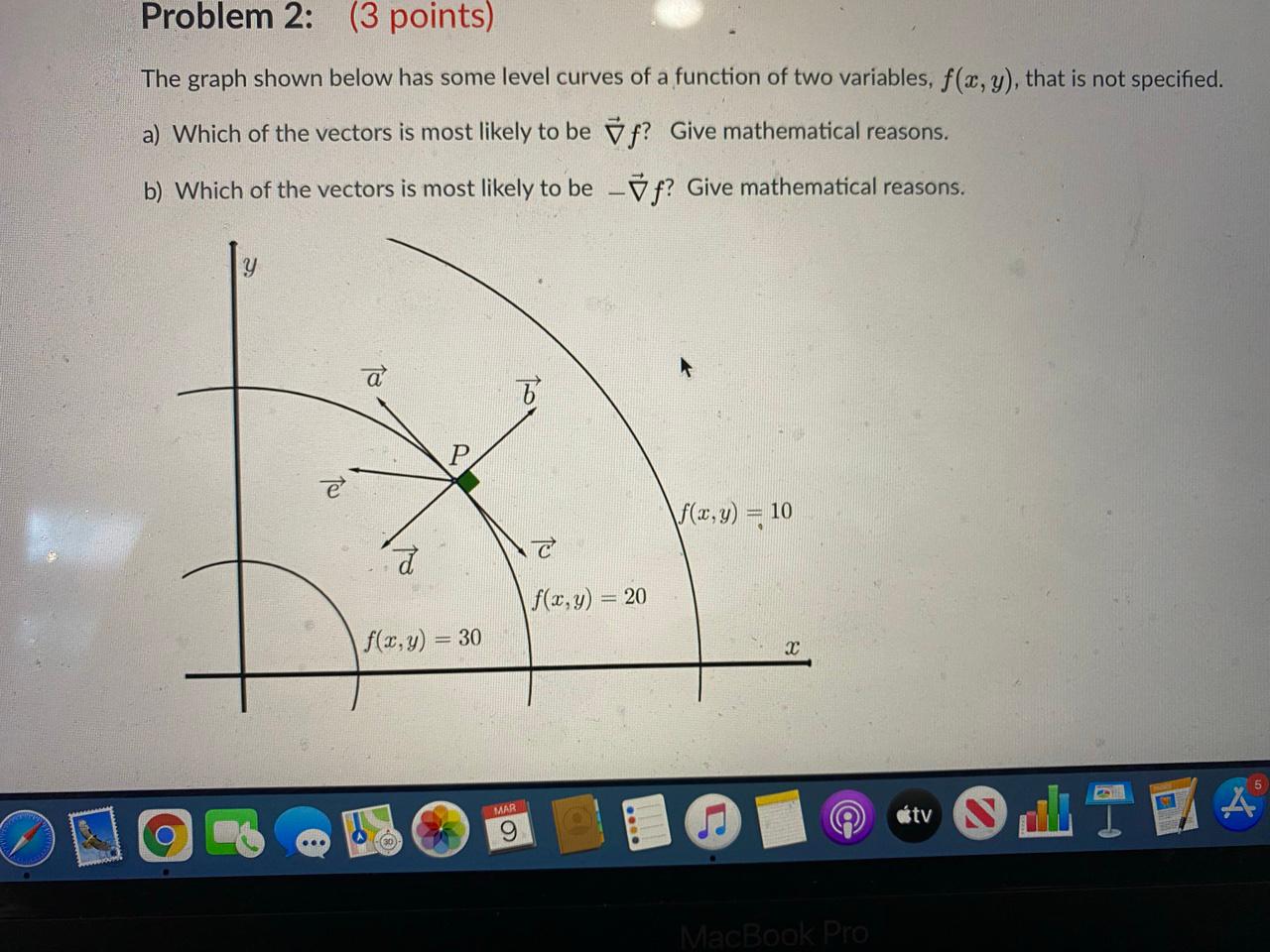



Problem 2 3 Points The Graph Shown Below Has Some Chegg Com




Chapter 14 Partial Derivatives 14 1 Functions Of Several Variables 1 Objectives Use Differential Calculus To Evaluate Functions Of Several Variables Ppt Download
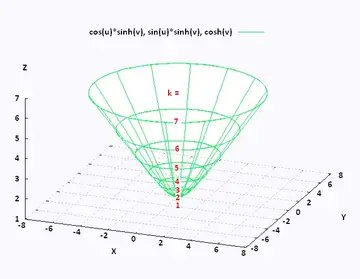



Mathematics Calculus Iii
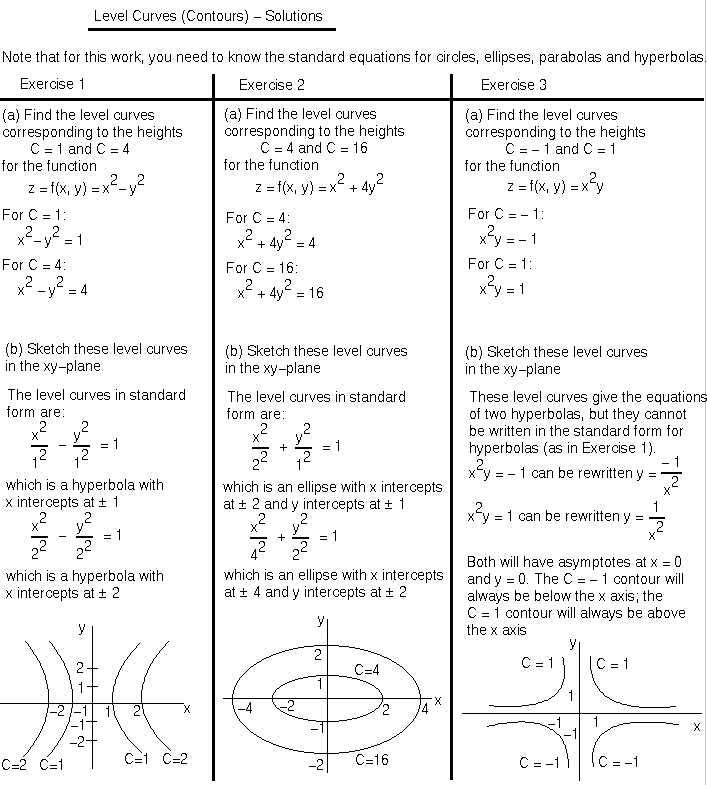



Functions Of Two Variables Math100 Revision Exercises Resources Mathematics And Statistics University Of Canterbury New Zealand




Level Curves And Implicit Differentiation Studocu



Calculus Iii Functions Of Several Variables




Calculus Iii Functions Of Several Variables



Contour Plot
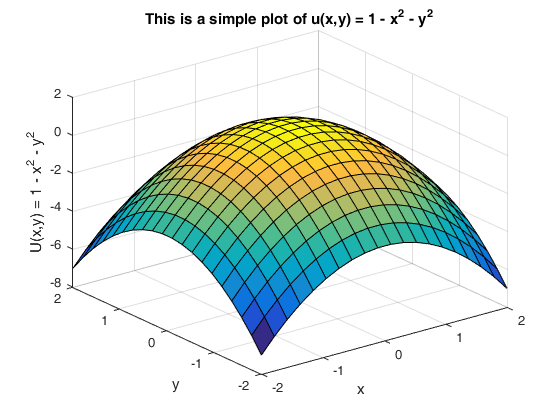



Howtoplotfunctiontwovariables



Lecture 4 Graph Level Curves Contour Lines Of Functions Of Two Variables Youtube
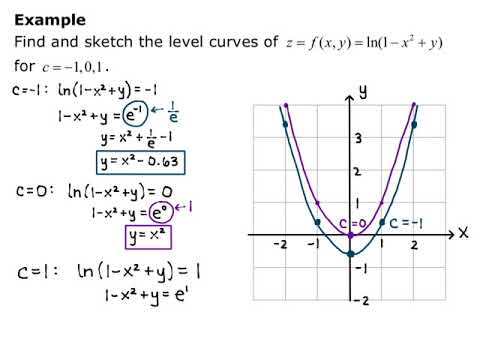



Section 13 1 Level Curves Youtube



The Gradient And Directional Derivative




14 Partial Derivatives Copyright Cengage Learning All Rights



1



Http Mathcs Holycross Edu Groberts Courses Ma241 Classroom Ch11 Functions Pdf



Math Tutor Extra Functions Of More Variables




Level Curves




Calculus Iii Functions Of Several Variables



Business Calculus




Calculus Iii Functions Of Several Variables




14 Partial Derivatives Partial Derivatives So Far We




13 1 Functions Of Several Variables Mathematics Libretexts



Www Usna Edu Users Oceano Raylee Sm223 Ch14 1 Stewart 16 Pdf



S0 3



15 1 Graphs And Level Curves 927 A Figure 15 18 Chegg Com



S0 3




Level Sets Math Insight




Ppt Functions Of Several Variables Partial Derivatives Powerpoint Presentation Id



Www Usna Edu Users Oceano Raylee Sm223 Ch14 1 Stewart 16 Pdf



Http Abel Math Harvard Edu Knill Teaching Summer14 Handouts Week2 Pdf




16 1 Functions Of Several Variables




1 Describe The Level Curves Of The Function Z 2x2 Chegg Com



0 3 Visualizing Functions Of Several Variables
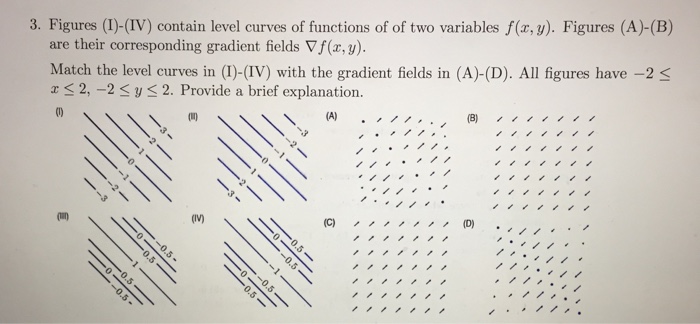



Figures I Iv Contain Level Curves Of Functions Of Chegg Com
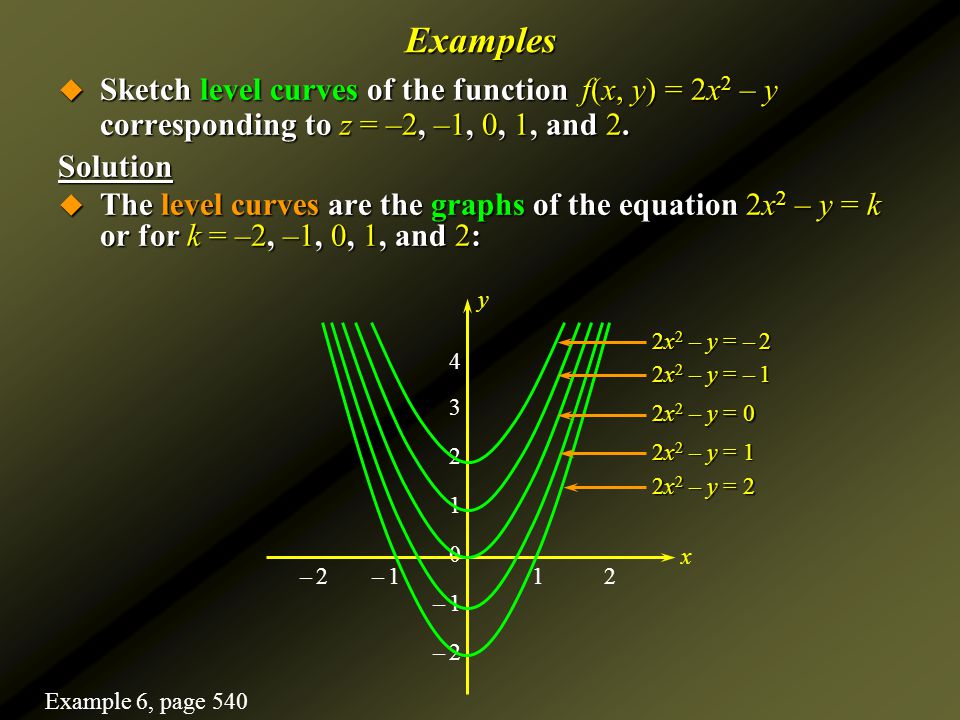



8 Calculus Of Several Variables Functions Of Several Variables Ppt Download



S0 3




Level Curves



Www Math Uci Edu Remote Teaching Lecture Notes Of Hamed Math 2d lecture notes Lecture note 14 1 Pdf




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




11 Level Curves And Contour Lines Of Functions Of Two Variables Youtube



Functions Of Two Variables Lessons Blendspace




3 D Calculus Continuous Function Function Mathematics
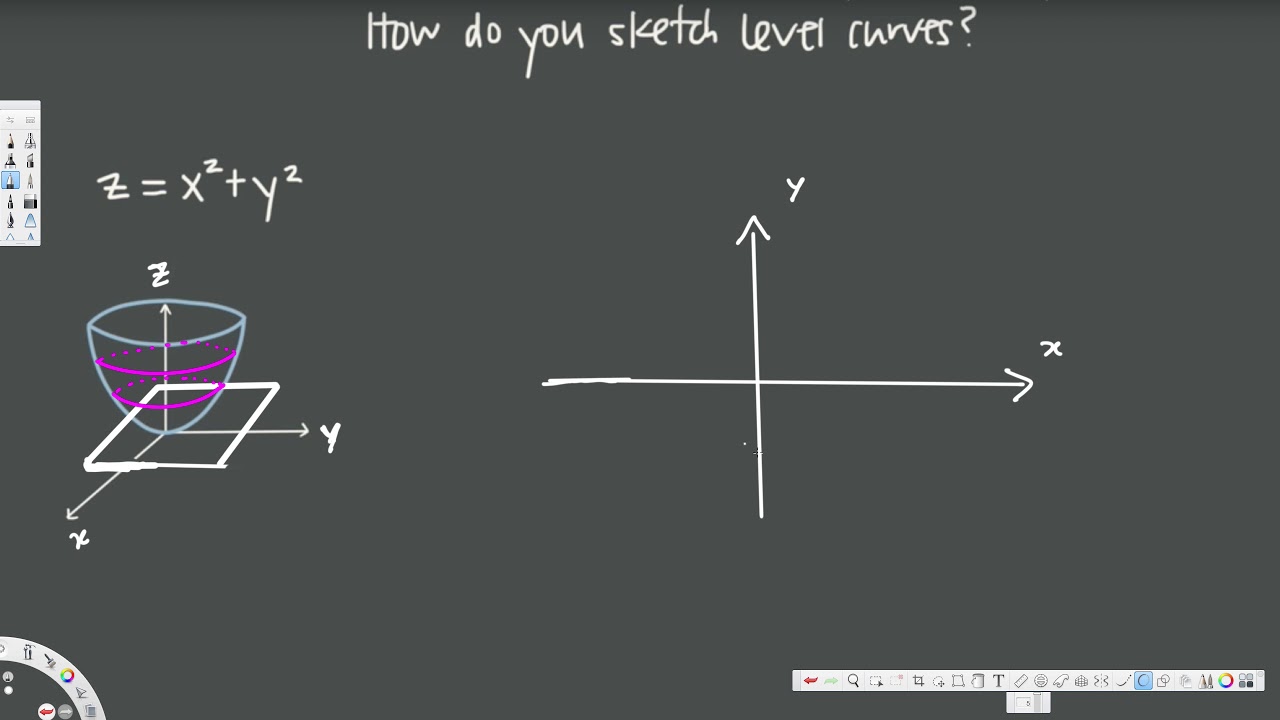



How Do You Sketch Level Curves Of Multivariable Functions Vector Calculus 1 Youtube
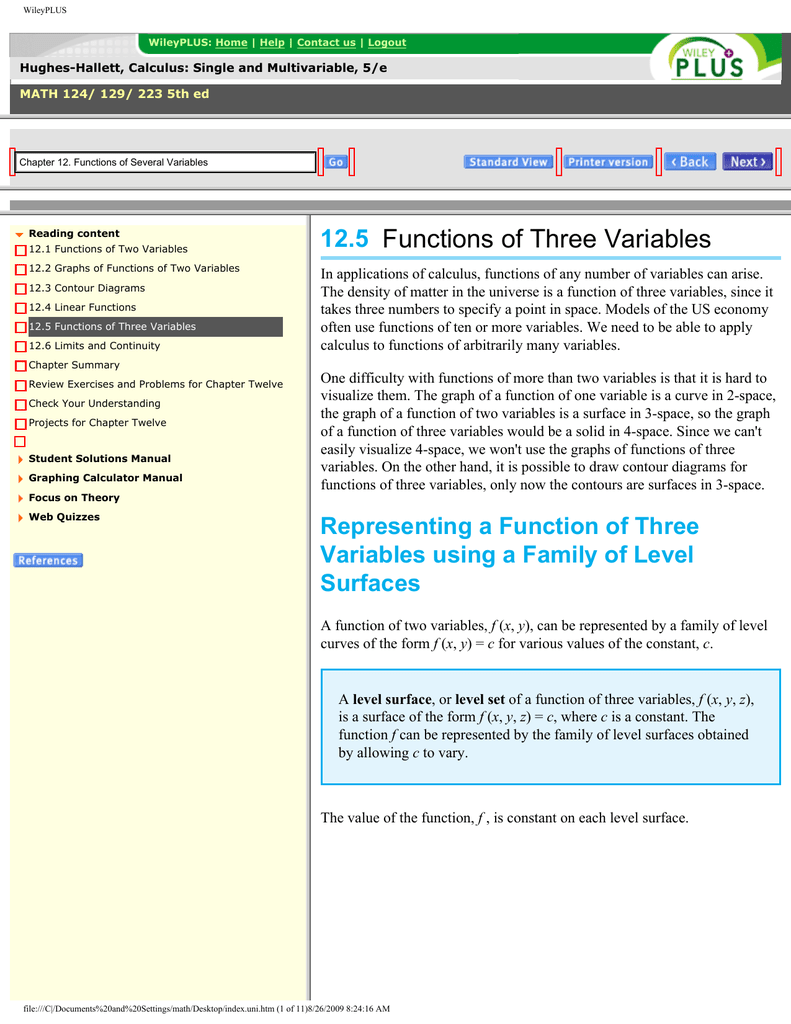



12 5 Functions Of Three Variables



0 件のコメント:
コメントを投稿